这篇需要常复习。

1.坐标系

笛卡尔坐标系

2D 坐标系

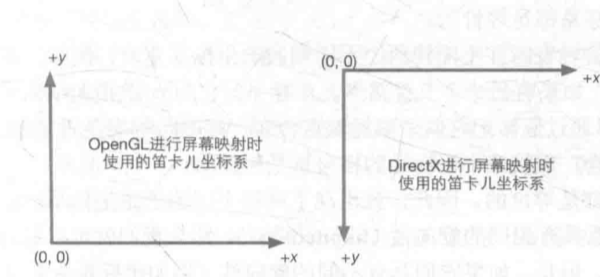
3D 坐标系

1.左手坐标系

Unity的左手坐标系，y上z前x右

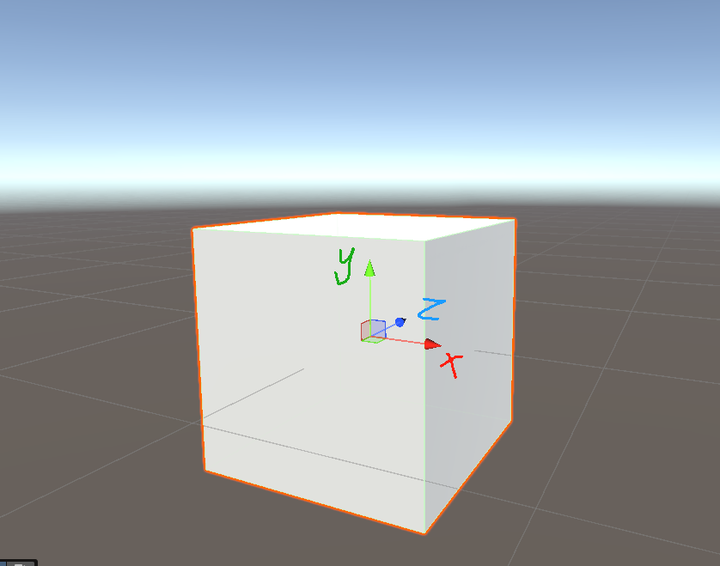
UE的左手坐标系，z上y右x前，相当于untiy的坐标系翻了一下，但仍然是左手。

2.右手坐标系

y上z后x右

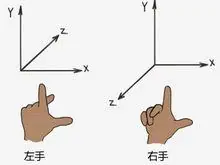
OpenGL：右手

DX：左手

3.疑问：

Q：左手坐标系如何转换右手？

—-A：z取负即可

Q：左右手坐标系，和矩阵使用行列向量是否有关系？

—-A：没有关系，UE使用行向量，Unity使用列向量，但都是左手

极坐标系

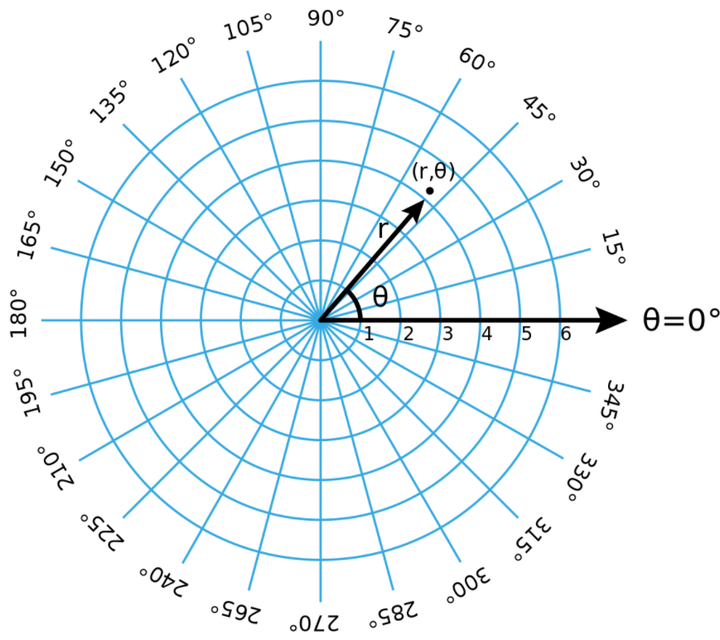
笛卡尔——>极坐标系

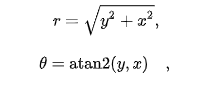
极坐标系——>笛卡尔

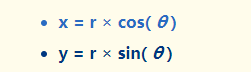
3D极坐标系

3d的极坐标系之前也接触过，做IK旋转的时候，正常笛卡尔无法做角度Lerp，转换到极坐标系进行角度的Lerp。

基本和2d的一样，找一下wiki里的公式转换就行。

2.向量

Position

比如在一个3d坐标空间，通常使用一个float3(x,y,z)表示这个点的位置Position。

这里直接也引入齐次坐标，如果表示一个点位置，它此时齐次坐标为

float4(x,y,z,1) w=1

转换为非齐次：
float3(x/1,y/1,z/1)

Vector

比如在一个3d坐标空间，使用一个float3(x,y,z)表示一个方向Vector。

这里也引入齐次坐标，如果表示一个方向，齐次坐标为

float4(x,y,z,0) w=0

vector和position的运算

vector和pos经常是有运算的，一般我们也是按照位置和方向区分，但是Games101这个图带来个新的震撼。

虽然point + point这个日常没使用过，但是数学概念是中点。

向量的运算

向量的大小：模

两点之间距离

两个点之间的距离是一个标量。实际上求模。

A（a，b，c） B（x，y，z）

AB之间距离为：B-A这个向量的模。

向量的加减

[a,b,c] + [x,y,z] = [a+x,b+y,c+z]

[a,b,c] - [x,y,z] = [a-x,b-y,c-z]

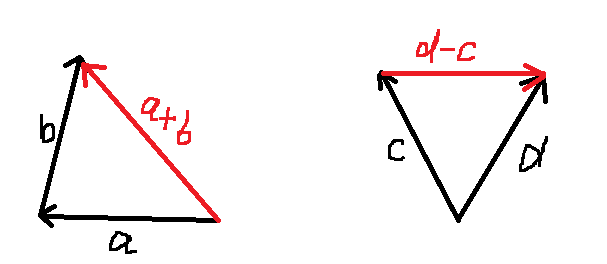
一个点到另一个点的向量

A（a，b，c） B（x，y，z）

（x-a，y-b，z-c） ——-> [x-a,y-b,z-c]

向量点乘Dot

Vector * 标量 = Vector

Vector * Vector = 结果为标量，值的意义一般是看Cos<A,B>

A（a，b，c） * B（x，y，z）

(a,b,c) · (x,y,z) = ax+by+cz

A · B = |A| |B| cos<A,B>

–	–	–
Dot>0	0°<= <a,b> <=90°	a和b方向基本相同
Dot=0	<a,b>=90°	a和b垂直
Dot<0	90°<= <a,b> <=180°	a和b方向基本相反

向量投影

b在a上的投影

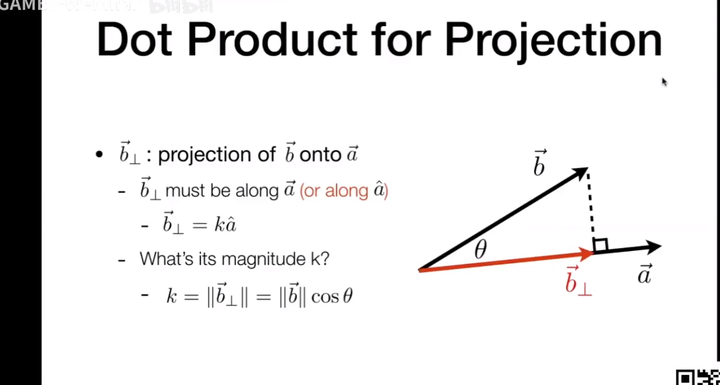
向量叉乘Cross

vector x vector = vector 结果为向量，垂直于AB所在平面

A(x1，y1，z1) x B(x2，y2，z2) =

(y1z2-z1y2 , z1x2-x1z2 ,x1y2-y1x2)

–如果Cross结果为零向量，说明AB平行。

–判断AxB结果与AB平面的方向

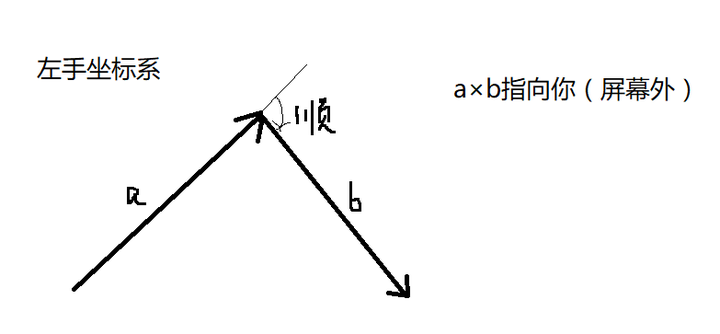
在左手坐标系中，a和b顺时针，那a×b指向屏幕外；逆时针则指向屏幕内；

右手坐标系相反；

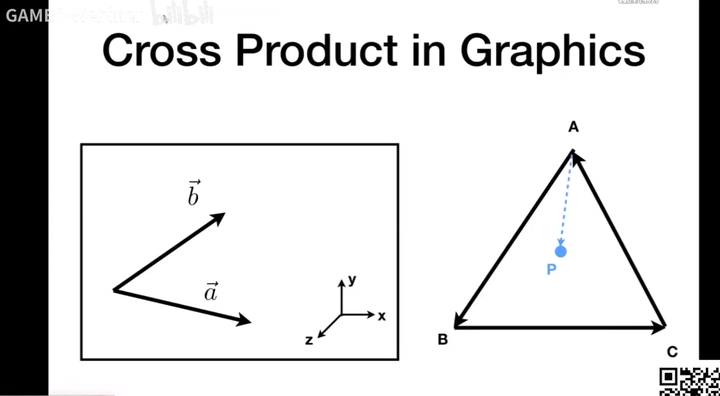
判断一个点是否在三角形内？

使用Cross运算，三条边与三个点到目标点的向量叉乘，同为正或同为负则在三角形内。

AB x AP

BC x BP

CA x CP

3.矩阵

矩阵的表示

向量是标量的数组。

矩阵是向量的数组。

矩阵的表示就是一组向量。

转置矩阵、逆矩阵、正交矩阵

转置矩阵

把行向量转换为列向量。

2x3矩阵的转置矩阵就是3x2矩阵。

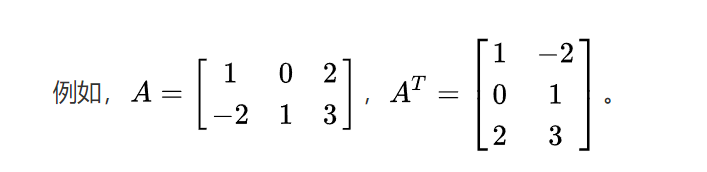
逆矩阵

设A是一个n阶矩阵，若存在另一个n阶矩阵B，使得： AB=BA=E（E为单位矩阵）

并不是所有矩阵都可逆。

正交矩阵

转置和逆矩阵一样的矩阵。

矩阵的运算

矩阵乘法

一个m×n矩阵A只能和n×c矩阵B相乘，得到m×c矩阵C；

一个2×3矩阵A和3×2矩阵B相乘，得到2×2矩阵C；

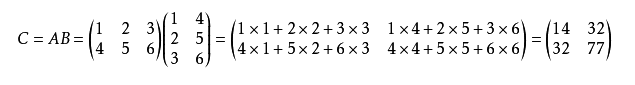
但是还是方阵乘法用的最多。

向量和矩阵乘法

向量能和矩阵乘，实际上把向量当成了一个维度是1的矩阵。

比如 1x3的向量可以乘 3x3 的矩阵 = 1x3向量。（最常见的一种了把，实际上是线性变换）

常见的数学表示，行优先（UE引擎）：

列优先，矩阵表示，(Unity引擎)：

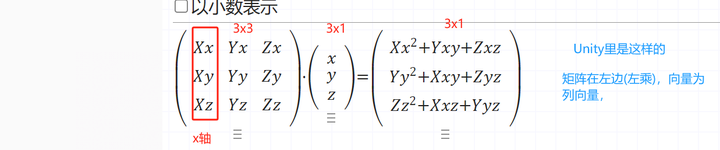
方阵与线性变换

平时用到最多的就是方阵，它可以表示线性变换(旋转、缩放、投影、镜像、仿射主要是中心不变)。

从一个坐标系转换到另一个坐标系(用三个XYZ基向量表示)。

这个矩阵就是表示线性变换的矩阵，把向量转换到新的坐标系。新的坐标系的3个基向量的表示按照原坐标计算。

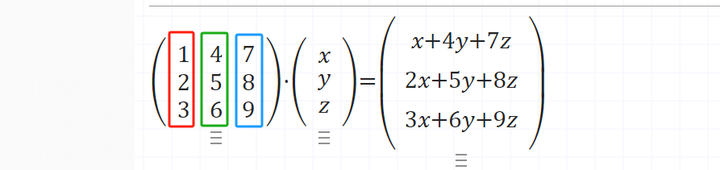
矩阵的推导

前面知道了线性变换时，矩阵其实就是3个基向量，那么来推导几个矩阵。

推导就是按照当前坐标系，算出目标坐标系的三个基向量。

下面都是按照Unity里的列优先矩阵写的。

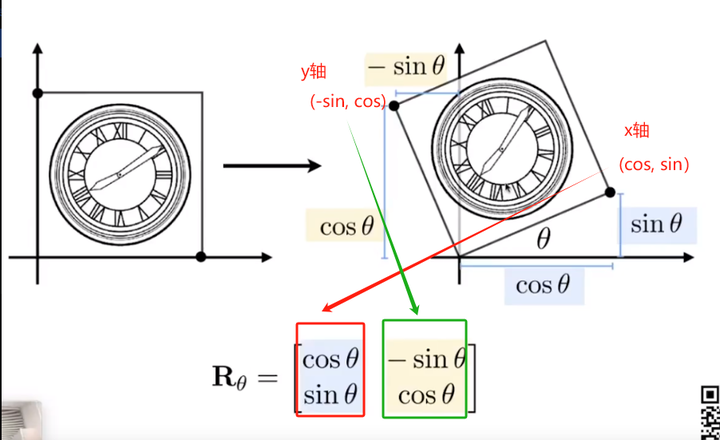
旋转矩阵

缩放矩阵

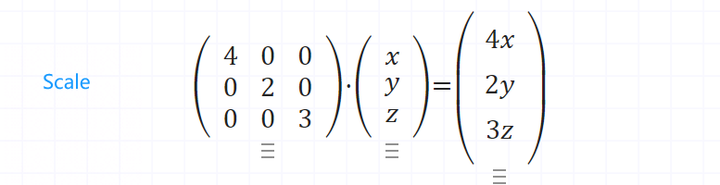
投影矩阵

投影意味着降维，某个分量是0。这种相当于直接丢失Z轴。

切变矩阵

一种坐标系的扭曲变换，非均匀拉伸；切变角度会发生改变，面积和体积不变；

基本思想：将某一坐标的乘积加到其他坐标上；

如：2D中，将y乘以某个因子a后加到x上，x’ = x+ay y’ = y

齐次矩阵

正常的3x3矩阵无法表示3d空间的平移，所以引入了齐次矩阵。

加入一个维度w，position的w默认为1，vector的w默认为0。

所以在齐次坐标表示的情况下，实际的3D点被认为是w=1的时候。
也就是(x/w, y/w, z/w, 1) w=1

在引擎里，MVP之后的齐次空间，w是不为1的，就可以表示出近大远小的感觉。

平移矩阵

Unity里写法

UE里写法

投影

齐次空间投影，如(x,y,z,w)向z = d投影

数学表示(右乘)：

透视和正交投影在后面坐标空间写。

4.方位和角位移

用矩阵和四元数来表示 “角位移”，用欧拉角表示“方位”。

矩阵表示

一般不用矩阵表示。

欧拉角

Unity内旋顺序： Y X Z

有万向锁问题。

四元数

引擎内部旋转都使用四元数，旋转唯一性，可以平滑Lerp。

5.球面UV

有时候需要将坐标转换为球面上的UV坐标进行某些计算，比如摇杆的输入信号。

/// <summary>
/// 将xy坐标转为球型uv坐标
/// </summary>
protected Vector2 SquareToCircle(Vector2 input)
{
    Vector2 output;
    output.x = input.x * Mathf.Sqrt(1 - (input.y * input.y) / 2);
    output.y = input.y * Mathf.Sqrt(1 - (input.x * input.x) / 2);
    return output;
}

6.三角形重心坐标

算出三角形的重心坐标，满足一个公式，所以重心坐标用(α，β，γ)分别表示ABC的权重。

由此，知道三角形三个点的数据，可以求出三角形中任意一点的uv、深度、color等信息。

7.计算反射

通过入射光和法线，求反射方向。

EB = N * |AB|cosθ = N * dot（N，AB）

DC = 2 * EB = -2 * N * dot(N, AB)

AC = AD + DC = -AB + 2 * N * dot（N，AB）

原理 Base